色yeye在线视频观看_亚洲人亚洲精品成人网站_一级毛片免费播放_91精品一区二区中文字幕_一区二区三区日本视频_成人性生交大免费看

優(yōu)化器(optimizer)

目標(biāo):  最小化損失函數(shù)

過程： 在反向傳播中,  根據(jù)學(xué)習(xí)率(lr)來對參數(shù)進行更新，最終逐步降低損失函數(shù)的大小, 使得神經(jīng)網(wǎng)絡(luò)輸出更好(函數(shù)擬合的更好)

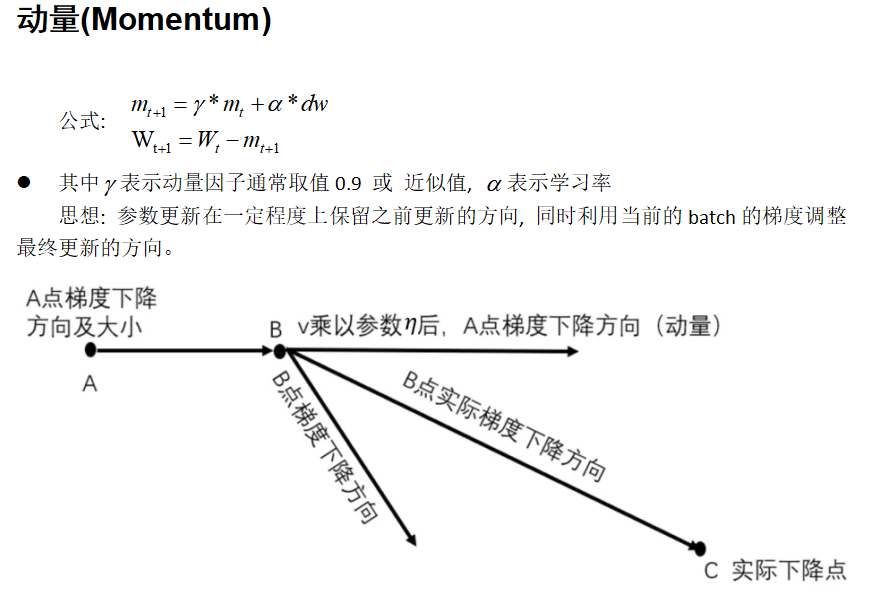
優(yōu)點:

1. 前后梯度一致時能夠加速學(xué)習(xí)

2. 前后梯度不一致時能夠抑制震蕩, 越過局部最小值

缺點:

1. 引入一個額外的參數(shù) y

思想: 結(jié)合Momentum和RMSprop兩種優(yōu)化器的算法, 并引入一階矩估計和二階矩估計。

優(yōu)點:

1. Adam能夠自動調(diào)整每個參數(shù)的學(xué)習(xí)率, 能夠很好地處理噪聲和非平穩(wěn)的訓(xùn)練數(shù)據(jù)

2. 相較于其他可變學(xué)習(xí)率(AdaGrad)的優(yōu)化器, 提高了訓(xùn)練速度

總結(jié)：

如果在未知模型上進行訓(xùn)練, 可以先考慮使用Adam確保損失函數(shù)能夠找到最小值, 即模型擬合的函數(shù)能夠收斂,然后切換回SGD進行訓(xùn)練, 快速達到對應(yīng)的值。