排序:
我們為何要研究排序?
1. 有時候應用程序本身需要對信息進行排序。
2. 許多程序把排序程序作為關鍵子程序。
3. 排序是我們學習編程的基本的訓練,對于程序的優化有很重要的作用。
我們之前已經學過簡單排序法和冒泡排序法。接下來我們介紹一下插入排序和合并排序。
1. 插入排序
輸入:n個數(a 1 ,a 2 ,.....a n)
輸出:輸入序列的一個排序(b1,b2....bn),使得b1 <= b2 <=....<=bn
插入排序的機制和打牌時整理手中的牌做法差不多。摸牌的時候,需要將摸到的牌插入到手中一把牌中的正確的位置上。為了要找到這張牌的位置,我們需要將它與手中每張牌從右到左進行比較。無論何時,左手中的牌都是排好序的。
這個算法中,所有的元素都是原地排序(sorted in place),就意味著這些數字就是在數組本身中重新排序的。
算法如下:
1、數組被分為兩部分,一部分為排好序的,一部分為未排好序。
2、選取一個key值,就是將要排序的元素,通過比較方式,將其插入到已排好順序的部分。
3、循環處理,直到該數組全部排好序。
偽代碼:
代碼(c語言實現):

//a 是一個數組,size_a是這個數組的元素個數
void insertion_sort( int * a, int size_a){
int i,j;
int key = 0 ;
for (j = 1 ;j < size_a;j ++ ){
key = a[j];
i = j - 1 ;
while (i > = 0 << a[i] > key){
a[i + 1 ] = a[i];
i = i - 1 ;
}
a[i + 1 ] = key;
}
return ;
}
插入排序算法的時間復雜度是O(n 2 ) 。當然算法的執行速度,和n的大小(輸入規模)以及樣本的結構有關系。考慮壞的情況,就是輸入的n個數為逆序排列,此時插入排序算法,隨著n的增大,運算時間的增長與 n 2 同數量級。
2.分治法策略
很多算法在結構上是遞歸的:為了解決一個給定的問題,算法要一次或多次地遞歸調用其自身來解決相關的子問題。這些算法通常采用分治策略:將原問題劃分為n個規模較小而結構與原問題相似的子問題;遞歸地解決這些子問題,然后再合并其結果,就得到原問題的解。
分治模式在每一層遞歸上都有三個步驟:
分解(divide):講原有問題分解成為一系列子問題;
解決(Conquer):遞歸地解各子問題。若子問題足夠小,則直接求解;
合并(Combine):講子問題的結果合并成原問題的解。
合并排序
合并排序的關鍵步驟在于合并步驟中的合并兩個已排序子序列。為做合并,引入一個輔助過程merge(a,p,q,r),其中a是一個數組,p,q和r是下標,滿足p <=q< r。該過程的子數組 a[p...q]和a[q+1.... r] 都已排好序,并將他們合并成一個已排好的子數組代替當前子數組a[p.....r]。
merge過程的代價是O(n)。其中n = r - p + 1是待合并的元素個數。
以下為合并的偽代碼:
為了能檢查兩個子數組是否是空,其想法是在每一個數組底部放一個“哨兵”,它包含了特殊值,用于簡化代碼。
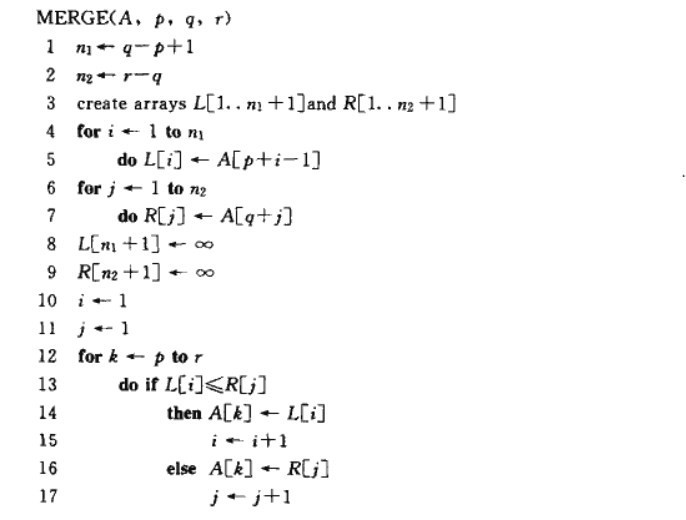
具體來說,merge過程是這樣工作的:第一行計算子數組a[p...q]的長度n1,第二行計算子數組a[q+1...r]的長度n2.在第三行中,創建了數組L和R,長度各位n1 +1,n2 + 1.第四到第五行中的for循環將子數組a[p...q]復制到L[1....n1]中去。 第六到第七行中的for循環將子數組a[q+1...r]復制到R[1....n2]中去。第八九行講哨兵置于L和R的末尾。第十到第十七行,是合并的具體過程。通過比較,將兩子數組按照從小到大的方式合并,存入數組A中。
c語言描述如下所示
void merge( int * a, int p, int q, int r){
int n1 = q - p + 1 ;
int n2 = r - q;
//為左數組和右數組分配空間,為max預留空間。
//max為哨兵,標志數組的結束。
int * L = ( int * )malloc( sizeof ( int ) * (n1 + 1 ));
int * R = ( int * )malloc( sizeof ( int ) * (n2 + 1 ));
for ( int i = 0 ;i < n1;i ++ ){
L[i] = a[p + i];
&nnbsp; }
for ( int i = 0 ;i < n2;i ++ ){
R[i] = a[q + i + 1 ];
}
L[n1] = MAX;
R[n2] = MAX;
//從小到大將左數組和友數組合并。
int i,j,k;
for (i = 0 ,j = 0 ,k = p;k < = r;k ++ ){
if (L[i] < = R[j]){
a[k] = L[i];
i ++ ;
} else {
a[k] = R[j];
j ++ ;
}
}
free(L);
L = NULL;
free(R);
R = NULL;
return ;
}
合并merge過程就可以作為合并排序中的一個子程序來使用。偽代碼如下:

c語言描述過程為:
void merge_sort( int * a, int p, int r){
int q = 0 ;
if (p < r){
q= (p + r) / 2 ;
merge_sort(a,p,q);
&nbsnbsp; merge_sort(a,q + 1 ,r);
merge(a,p,q,r);
}
return ;
}
合并程序的具體圖示:
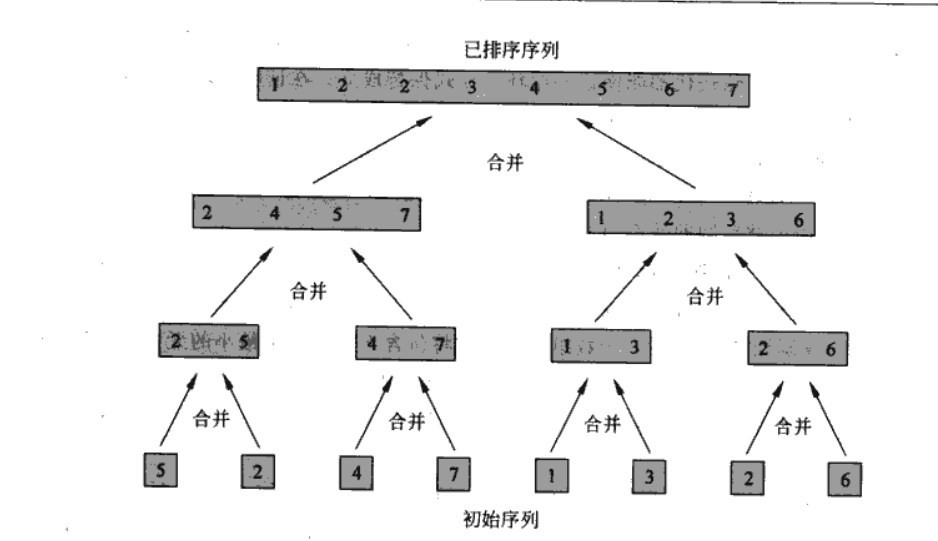
關于分治法排序的簡要分析:
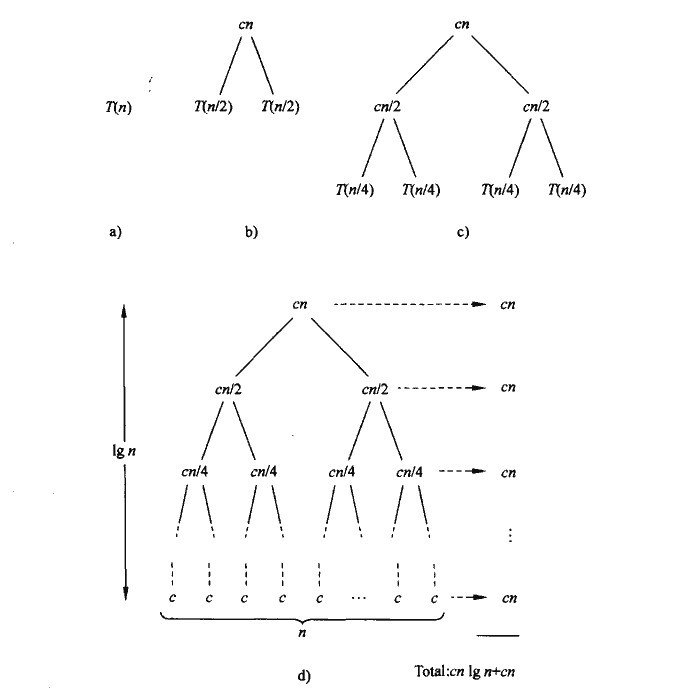
我們將一個規模為n的問題,拆分成n個規模為1的子問題。拆分的過程經歷了
lg n + 1層,在合并時,每一層的問題規模為n,則總代價為O (n * lg n + n ) ,忽略低階項和常數項,因此合并排序法的時間復雜度為O(n lg n )。
接下來會介紹一下堆排序和快速排序。以上的所有排序方法,都是比較排序。也就是說,他們通過對數組元素比較來實現排序。比較排序法是有極限的,從壞的輸入情況,比較排序法的時間復雜度是 O(n lg n )。我們介紹的合并排序以及快速排序,都是漸進優的比較排序方式。我們還會介紹可以突破比較排序極限的排序方式——計數排序。