 斯特拉森矩陣乘法簡介
時間:2018-08-15 來源:未知
斯特拉森矩陣乘法簡介
時間:2018-08-15 來源:未知
二維數組無論在數值計算領域還是在非數值計算領域都是一種相當基本、重要且抽象的數據結構。二維數組在數學中的表現形式是矩陣,因此研究 矩陣的基本運算本質上就是在研究二維數組的運算。顯然,盡可能地提高矩陣運算速率對于編程而言是十分重要的工作。
矩陣加法和矩陣乘法是矩陣中基本的矩陣運算。設A、B是兩個n×n的矩陣。矩陣的加法表示兩個矩陣對應位置元素之和,因此它們的和仍然是一 個n×n的矩陣,記為C=A+B。顯然,矩陣加法的時間復雜度為O(n2)。
如果設矩陣A與B的乘積為矩陣C,即C=A×B,顯然矩陣C也是一個n×n的矩陣。則矩陣C的第i行第j列的元素C(I,j)等于矩陣A的第i行和矩陣B的第j 列對應元素乘積的和。可表示為:
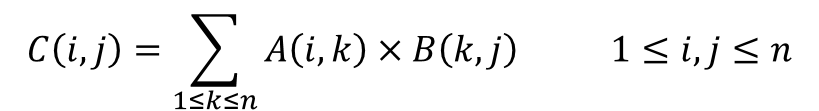
按這個公式計算C(i,j)需要n次乘法與n-1次加法,而矩陣C中有n×n個元素,因此,由矩陣乘法定義而直接產生的矩陣相乘算法時間復雜度為O(n3) 。
人們長期對矩陣的乘法計算的改進工作做著不懈的努力,做出不少嘗試,也試圖設計或改進這個算法,但無論怎樣改進都囿于O(n3)數量級的時間 復雜度,沒有顯著地提速。
1969年,斯特拉森(V.Strassen)利用分治策略并加上數學處理設計出了一種時間復雜度是O(n2.81)(準確地說是O(nlog7))的矩陣相乘算法,宣 稱在時間復雜度數量級上有所突破。此結果一發布,立即震動了整個數學界。
為簡單描述這一算法,我們假定矩陣C的階數是2的冪,即存在一個非負正數k使得n=2k。若n不是2的冪,則可通過適當添加全零行和全零列來構造 成2的冪的方陣。
按照分治策略,首先將矩陣A與B分解成4個(n/2)×(n/2)矩陣,即:
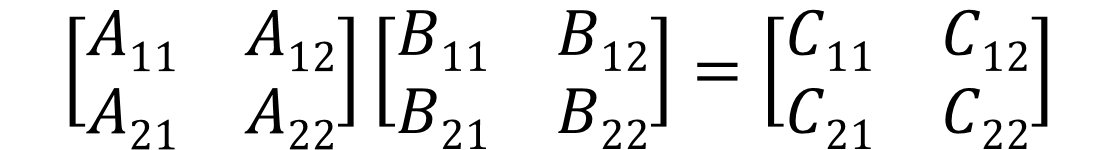
對A和B每個(n/2)×(n/2)矩陣進行矩陣乘法運算即可得到C。其中:
C11=A11B11+A12B21
C12=A11B12+A12B22
C21=A21B11+A22B21
C22=A21B12+A22B22
使用通常的矩陣乘法與加法計算分別得到C11、C12、C21、C22四個子矩陣,那么顯然可以得出分塊子矩陣拼接后的矩陣就是矩陣C。如果分塊子矩陣階 數仍然大于2,則可繼續用此方式將分塊子矩陣劃分為更小的4塊,直至每個子矩陣都只有1個元素以至于可以直接計算其乘積為止。對于使用分塊子矩 陣計算C的方法,顯然需要8次乘法與4次加法,由于每兩個n/2級方陣的計算都可以在某個可預見的時間cn2(c是常數)內完成,則通過分治法我們可 以得到T(n)的遞歸表示方法:
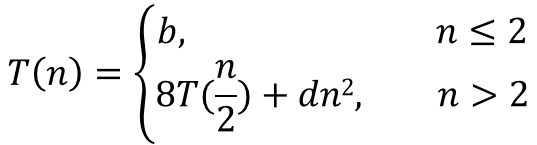
其中b和d是兩個常數。求解這個遞歸關系式:
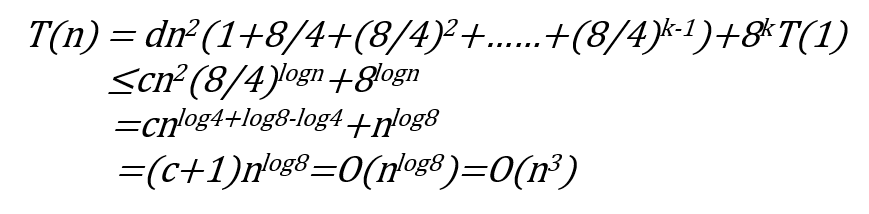
可以看出,這種方式與通常的矩陣乘法計算時間復雜度一樣。究其原因,這種方法仍然是使用8次乘法與4次加法。若無法有效降低乘法的次數,則仍 然無法有效降低時間復雜度。
斯特拉森在分治法的基礎上,設計出了一種7次乘法的處理方式。其處理方式是:先使用7個乘法10個加法計算7個等式:
P=(A11+A22)(B11+B22)
Q=(A21+A22)B11
R=A11(B12-B22)
S=A22(B21-B11)
T=(A11+A12)B22
U=(A21-A11)(B11+B12)
V=(A12-A22)(B21+B22)
然后使用8個加法將這7個等式構造成C:
C11=P+S-T+V
C12=R+T
C21=Q+S
C22=P+R-Q+U
以上共使用7次乘法與18次加法。
則由T(n)所得的遞歸公式是:
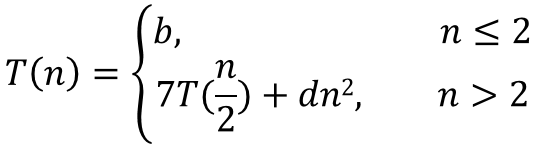
推導時間復雜度的過程類似上文,這里不再贅述。終可得時間復雜度為O(nlog7)≈O(n2.81)。
在斯特拉森之后,許多人也試圖繼續改進該算法。其中,J.E.Hopcroft和L.R.Kerr已經證明,兩個2的冪階矩陣相乘必須要使用7次乘法無法再簡化。 若想再進一步簡化則必須考慮劃分為3的冪或4的冪以及更高級的冪階才有意義。因此分治策略必須改變,即必須采取其他分治策略的設計思路才行。
后需要說明的是,斯特拉森矩陣乘法目前只有理論意義。事實證明當矩陣階數足夠大(n在128階以上)時,它和普通的矩陣乘法的執行時間仍無顯 著差別。即使如此,斯特拉森矩陣乘法給我們提供了一個有益的啟示:即使從簡單的定義出發來設計的算法也可能不是好的,仍然可以去優化。
參考文獻:
[1]《線性代數與多項式的快速算法》
[2]《計算機算法基礎(第三版)》

