 二叉樹基本概念講解及創(chuàng)建
時間:2018-08-16 來源:未知
二叉樹基本概念講解及創(chuàng)建
時間:2018-08-16 來源:未知
一、簡介
世界上的樹有千萬種,我們這里來學習我們數(shù)據(jù)結(jié)構(gòu)中的樹,它是我們現(xiàn)實生活中倒置的樹。之前,我們學習的順序表,鏈表,棧、和隊列。可以說都是我們的線性結(jié)構(gòu),也就是我們所謂的一對一的結(jié)構(gòu),可是現(xiàn)實生活中,我們經(jīng)常碰到是我們一對多的情況。今天,我們就來研究一下這種一對多的數(shù)據(jù)結(jié)構(gòu)體-----“樹”。那么,什么叫做樹呢?

二、樹的基本概念簡介
<1>樹的定義
專業(yè)定義:(1)有且只有一個稱為根的結(jié)點
(2)有若干不相交的子樹,這些子樹本身也是一顆樹。
通俗講解:
(1)樹由結(jié)點和邊組成
(2)樹中除根節(jié)點外,每一個節(jié)點都有一個父結(jié)點,但是 可以用多個子節(jié)點。
(3)根結(jié)點沒有父結(jié)點
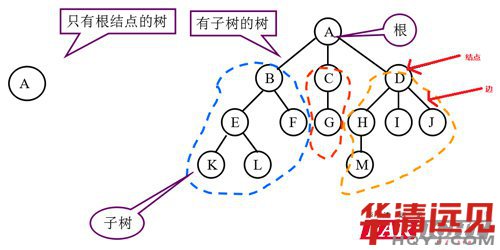
<2>樹中的專業(yè)術(shù)語
節(jié)點 : 父節(jié)點 子節(jié)點(老子和兒子) 堂兄弟
度: 結(jié)點擁有子樹的個數(shù)
葉子節(jié)點:沒有子節(jié)點的節(jié)點
邊 : 一個節(jié)點到另一個節(jié)點的距離
樹的深度:節(jié)點的層數(shù), 根節(jié)點默認為第一層。
有序 :樹的左右位置不能改變。
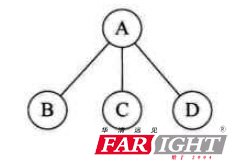
<3>樹的分類
一般樹 : 任意一個結(jié)點的子節(jié)點的個數(shù)不受限制,則稱為一般樹。(子節(jié)點可以有多個),如下圖:
二叉樹(重點):任意一個節(jié)點的子節(jié)點的個數(shù)多有兩個,且子節(jié)點的個數(shù)不能更改。
森林:樹去掉根結(jié)點就稱之為森林。
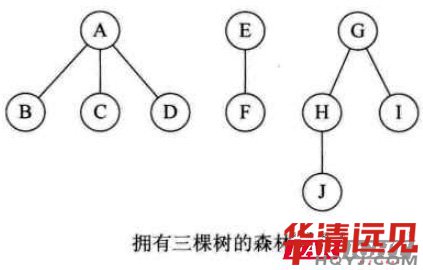
提問:在下圖中:
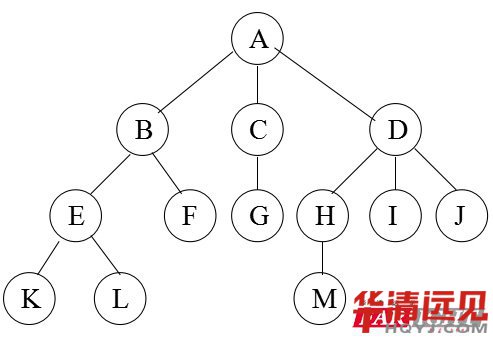
<1>A,B,H,I的度分別是多少?
A:3 B : 2 H: 1 I: 0
<2>葉子節(jié)點有哪些?
K ,L,F,G,H,I,J
<3>結(jié)點F和I在樹中的第幾層?
F在第3層。
M在第4層
<4>樹的深度是多少?
4
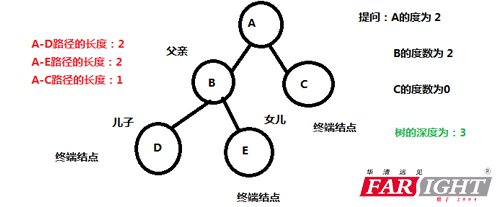
三、二叉樹的特性講解
<1>二叉樹的性質(zhì)講解
如下圖是一顆二叉樹,它有一些特性:
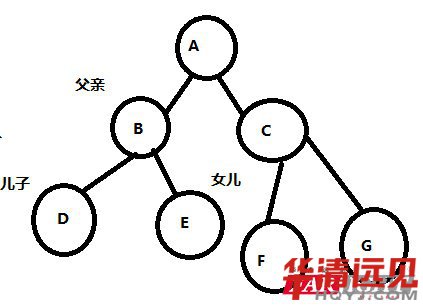
思考:第一層多有多少個? 1個
第二層多有多少個? 2 個
第三層多有多少個? 4 ?
規(guī)律:第i層結(jié)點后有2的n - 1次方個。
性質(zhì)1:二叉樹的第i層上的結(jié)點多有2的i - 1次方個節(jié)點。
思考:深度為1的二叉樹(遍歷第一層)一共有多少個節(jié)點? 1個
深度為2的二叉樹(遍歷到第二層)一共有多少個節(jié)點? 3個
深度為3的二叉樹(遍歷到第三層)一共有多少個節(jié)點? 7個
規(guī)律:深度為k的而出書,多有2的k次方 - 1個節(jié)點。
性質(zhì)2:深度為k的二叉樹多有2的k次方-1個結(jié)點。
性質(zhì)3:在任意一棵二叉樹中,樹葉的數(shù)目比度數(shù)為2的結(jié)點的數(shù)目多1.
(推導過程入下圖所示:)

<2>二叉樹的分類
滿二叉樹:在一顆二叉樹中,如果所有的分支節(jié)點都存在左子樹和右子樹,并且所有的葉子節(jié)點都在同一層上,這樣的二叉樹,我們稱之為滿二叉樹。
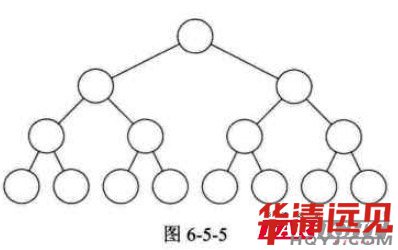
滿二叉樹的特點:<1>葉子節(jié)點只會出現(xiàn)在下面一層。
<2>非葉子節(jié)點的節(jié)點,擁有子樹的個數(shù)一定為2.
<3>在同樣深度的二叉樹中,滿二叉樹的節(jié)點個數(shù)多。
完全二叉樹:對一顆具有n個結(jié)點的二叉樹按層進行編號,如果編號為i
(1 <= i <= n)的結(jié)點與同樣深度的滿二叉樹節(jié)點編號為i的結(jié)點
在二叉樹中的位置完全相同,則這顆樹,我們稱之為完全二叉樹。
如下圖所示。
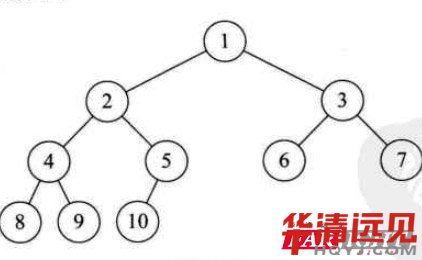
提問:下面這些樹,是完全二叉樹嗎? 不是
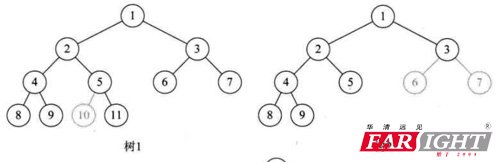
總結(jié):滿二叉樹一定是完全二叉樹,完全二叉樹不一定是滿二叉樹。
四、二叉樹的存儲
(1)順序存儲[完全二叉樹]
(順序存儲的話,若不是完全二叉樹存儲沒有意義。)
假設(shè)下面有一顆樹,我們?nèi)绾伟阉娴綌?shù)組中呢?
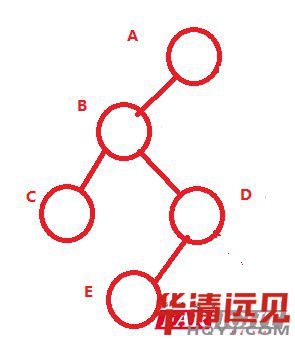
思路:先把轉(zhuǎn)換成完全二叉樹,然后再編號。
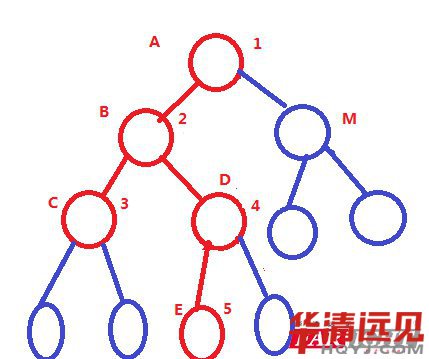
這樣存儲就看似沒有什么問題。我們可以按照編號把數(shù)據(jù)存儲到數(shù)組中,我們按照編號(1,2,3,4,5)的順序存儲就可以了啊!這個時候,我就要問了,假說說,我們的m的編號,你怎么知道我們的3好位置是在下面,而不是在我們的m編號的位置呢?我們的連續(xù)存儲無法識別。(這種方法,我們無法推斷樹的結(jié)構(gòu))。
因此,我們順序存儲規(guī)定:
無論是何種樹,我們都會轉(zhuǎn)換成完全二叉樹。然后一層一層的從左給我們的二叉樹進行編號,然后存儲在數(shù)組中。及如下圖。
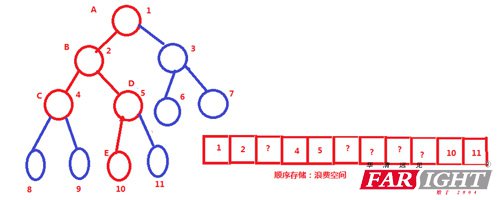
那么我們以上的存儲有什么規(guī)律呢?假設(shè)某個節(jié)點為i的話,我們來觀察一下。
是不是所有的左孩子都是偶數(shù),所有的右孩子都是奇數(shù)啊!
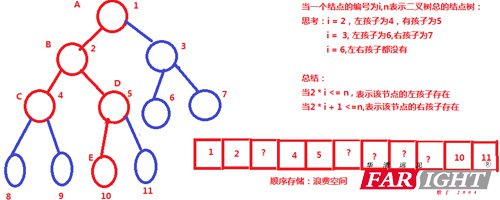
完全二叉樹的特點:
對于編號為i(i>=1)的結(jié)點:
(1)左孩子存在:2 * i <= n(節(jié)點的個數(shù)),左孩子編號
(2)右孩子存儲:2 * i + 1 <= n,右孩子編號 2 * i + 1
(2)鏈式存儲[完全二叉樹]
鏈式存儲:定義結(jié)點保存左孩子和右孩子的地址。
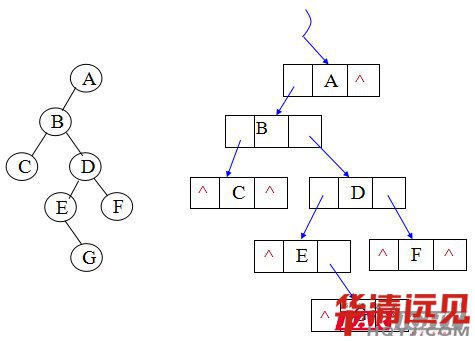
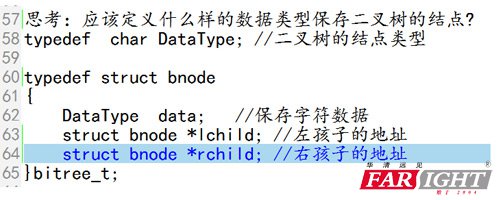
思考:上述過程,我們的二叉樹應(yīng)該定義什么樣的數(shù)據(jù)類型來保存結(jié)點呢?
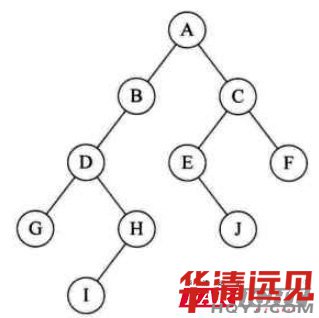
<4>二叉樹的遍歷
(1)層次遍歷:從上到下一層一層的遍歷
(2)前序遍歷:根 、左(左子樹)、右(右子樹)
(3)中序遍歷:左(左子樹) 、根 、右(右子樹)
(4)后序遍歷:左(左子樹)、右(右子樹)、根
規(guī)則:遇到根結(jié)點則輸出,否則遍歷。
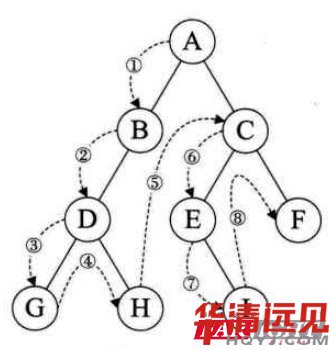
層次遍歷:ABCDEFGHI
先序遍歷:ABDGHCEIF
中序遍歷:GDHBAEICF
后序遍歷:GHDBIEFCA
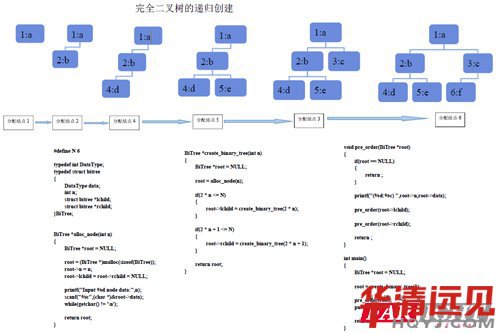
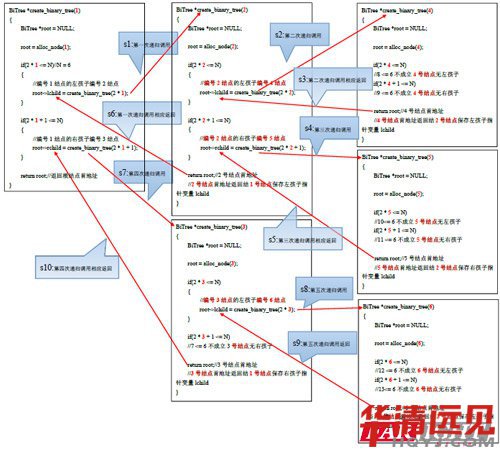
完全二叉樹的遞歸創(chuàng)建思路:
1.首先,寫一個創(chuàng)建單個節(jié)點的函數(shù)malloc_bnode,左孩子和右孩子都為空并且填充,我們需要的數(shù)據(jù)
2.然后寫一個創(chuàng)建二叉樹的函數(shù)create_binarytree()函數(shù)。調(diào)用malloc_bond
函數(shù)創(chuàng)建節(jié)點,然后判斷結(jié)點有沒有左孩子和右孩子。
2 *num <= n ,左孩子存在 (num為我們的結(jié)點編號,n為我們的結(jié)點個數(shù))
再次,調(diào)用create_binarytree()創(chuàng)建該編號的孩子。
2 *num + 1 <=n,右孩子存儲。
再次,調(diào)用create_binarytree()創(chuàng)建該編號的孩子,后返回根節(jié)點。
二叉樹相關(guān)文章:

