排序與排序算法
時間:2018-09-26 來源:未知
排序與排序算法
時間:2018-09-26 來源:未知
一、排序的基本概念與分類
1、排序的定義
假設含有n個記錄的序列為{r1,r2,……rn},其相對應的關鍵字分別為{k1,k2,……kn},需確定一種序列,使其關鍵字滿足k1<=k2<=……<=km(非遞減)或k1>=k2>=……>=km(非遞增)關系,即使得序列成為一個按關鍵字有序的序列{r1,r2,……,rm},這樣的操作就稱為排序。
排序的依據是關鍵字之間的大小關系,那么,對于同一個記錄集合,針對不同的關鍵字進行排序,可以得到不同的序列。
2、排序的穩定性。
假設在排序前,有ki=kj(1<=i<=n,1<=j<=n,i不等于j),且在排序前的序列中ri位置于rj(即i
例如有序列:
編號 姓名 總分
1 Li 750
2 Liu 730
3 Zhou 738
4 Han 750
此時我們按總分排序,如果得到
1 Li 750
4 Han 750
2 Zhou 738
3 Liu 730
這樣排序算法就是穩定的。而如果得到
4 Han 750
1 Li 750
2 Zhou 738
3 Liu 730
則這樣的排序算法就是不穩定的。
對于多個關鍵字排序時,如果有一組關鍵字會得到不穩定的結果,則我們就認為此排序算法是不穩定的。
3、排序算法的分類
1)按數據位置分類
根據排序過程中待排數據是否全部被放置在內存中,排序分為:內排序和外排序
內排序:排序過程中,待排數據全部被放置在內存中。
外排序:排序過程中,因記錄太多,不能同時放在內存中,整個排序過程中需要在內外存之間多次交換數據才能進行。
我們這里只討論內排序算法。對于內排序來說,排序算法的性能主要受3個方面影響:
⒈時間性能
排序是數據處理時經常執行的操作,往往屬于核心代碼部分,因此排序算法的時間開銷是衡量其好壞的重要標志。在排序中,主要涉及到兩種操作:比較與移動。高效率的排序算法應該是具有盡可能少的關鍵字比較次數和盡可能少的數據移動次數。
⒉輔助空間
評價排序算法的另一個主要標準是執行算法所需要的輔助空間。輔助存儲空間是除了存放待排序所占用的存儲空間之外,執行算法所需要的額外存儲空間。
⒊算法的復雜性
過于復雜的算法會影響其排序性能。
2)按排序操作分類
根據排序過程中借助的操作,我們把排序分為:插入排序、交換排序、選擇排序和歸并排序。
3)按算法的復雜性分類
根據排序算法的復雜性分類,可分為簡單排序算法和改進排序算法。
簡單排序算法:冒泡排序、直接選擇排序、直接插入排序
改進排序算法:Shell排序、堆排序、歸并排序、快速排序
//注:下文中涉及到的代碼詳見附錄
二、冒泡排序
無論學習哪種編程語言,當學習到循環與數組等概念的時候,通常會介紹一種排序算法來作為例子或練習。而這種排序算法通常都是冒泡排序。
1、簡單的冒泡排序
冒泡排序(Bubble Sort)是一種交換排序,它的基本思想是:兩兩比較相鄰記錄的關鍵字,如果反序則交換,直到沒有反序為止。
在排序過程中,較小的數字(或較大的數字)會如同水下的氣泡一樣慢慢浮出水面,冒泡排序的命名就此而來。
//代碼見附錄
2、冒泡排序優化1
冒泡排序是否可以進行優化呢?答案是肯定的。
試想,如果待排序數據是基本有序的(例如2,1,3,4,5,6,7,8,9,10,除了第一和第二個關鍵字不同,需要交換外,其他數據關鍵字都已經有序。此時我們只需交換這兩個數字即可,而無需將冒泡排序執行到底。
我們可以設置一個標志位flag,用它來指示一次冒泡排序執行后是否有數據交換。如果一次排序后沒有數據交換,我們就可以認為數據已經有序,無需再繼續執行后面的工作了。
//代碼見附錄
代碼改動的關鍵就是在外層循環for()的結束條件中,增加了對flag是否是true的判斷。這樣的改進能避免數據在有序的情況下做無意義的循環判斷,從而提升效率。
3、冒泡排序優化2
從另一個角度來想,一次循環數據從前掃描到后,然后再從前掃描到后……也就是說,“磁頭”掃描一個來回移動一個關鍵字使其有序。如果我們能在“磁頭”移動回表頭時,也能移動一個關鍵字,那么就相當于一次掃描一個來回移動兩個關鍵字,可以提升其執行效率。
//代碼見附錄
三、直接選擇排序
冒泡排序是基于比較和交換的排序,其算法思想就是不斷交換,通過交換完成終排序。而直接選擇排序則是基于選擇的排序,其算法思想是每次選出待排數據的關鍵字中大(或小)的數據作為第i個記錄。
1、直接選擇排序算法
選擇排序算法(Selection Sort)就是通過n-i次關鍵字比較,從n-i+1個數據中每次挑選出關鍵字小(或大)的數據并和第i(1<=i<=n)個數據交換之。
//代碼見附錄
注意代碼中的min是這次排序過程中小數據的下標。
從性能上來說,選擇排序略優于冒泡排序。
四、直接插入排序
撲克牌是我們都玩過的游戲。那么摸到手的撲克牌如何理牌呢?一般情況下,都是選出一張牌,將它放置在比它大和比它小的兩張牌之間。這里我們用于理牌的方法就是直接插入排序。
1、直接插入排序算法
直接插入排序算法(Straight Insertion Sort)的基本操作是將一個數據插入到一個已經排好序的有序表中,從而得到一個新的有序表。重復這個過程,直至所有數據有序。
//代碼見附錄
需要注意的是,直接插入排序需要一個已經有序的序列作為“基準”。代碼中,選區r[0]與r[1]作為基準,在排序前,需要判斷r[0]與r[1]的關系保證其是有序表。可以嘗試省略掉這一步,觀察排序后的內容。
從性能上來說,直接插入排序略優于冒泡排序。
五、快速排序
上文中介紹的的冒泡排序、選擇排序、直接插入排序及其改進版本,都屬于簡單排序算法。因為它們的時間復雜度都為O(n^2)。而改進排序算法(Shell排序、堆排序、歸并排序、快速排序)的時間復雜度都為O(nlog2n)甚至更快。在這里我們主要學習快速排序。
1、快速排序算法
快速排序算法早由圖靈獎獲得者Tony Hoare于1962年設計出來,被稱為“20世紀十大算法”之一。
快速排序相當于冒泡排序的升級,二者都屬于交換排序類。
快速排序(Quick Sort)的基本思想是:通過一趟排序將待排數據分割成獨立的兩部分,其中一部分的關鍵字都比另一部分的關鍵字小。之后對這兩部分分別進行排序,終達到整體有序。
快速排序算法的文字描述是:
1)設置兩個變量i、j,排序開始的時候:i=0,j=N-1;
2)以第一個數組元素作為關鍵數據,賦值給key,即key=A[0];
3)從j開始向前搜索,即由后開始向前搜索(j--),找到第一個小于key的值A[j],將A[j]和A[i]互換;
4)從i開始向后搜索,即由前開始向后搜索(i++),找到第一個大于key的A[i],將A[i]和A[j]互換;
5)重復第3、4步,直到i=j;此時令循環結束。將key值賦值到i(或j)的位置。
6)遞歸操作數組A[]在key值左的左半部分。
7)遞歸操作數組A[]在key值右的右半部分。
//代碼見附錄
2、快速排序算法的優缺點
快速排序算法之所以叫“快速”排序,意味著目前階段沒有人找到更優秀于這個算法的排序算法。如果某一天有人找到了更好的排序算法,“快速”就會名不副實,不過,至今為止,Tony Hoare發明的排序算法經過多次優化后,在整體性能上,依然是排序算法中的王者。
不過快速排序算法仍有缺陷,快速排序算法雖然對大數據排序十分擅長,但不擅長數據不多時進行排序。在數據不多時,快速排序與冒泡排序幾乎看不出時間上的優勢,只有數據足夠大時,快速排序才能發揮出它的優勢。因此我們在對數據進行排序時,若數據量不太多,可以選擇使用三種簡單排序算法(冒泡排序、選擇排序、直接插入排序);若數據量巨大,我們就需要選擇快速排序。
附錄1:各排序算法代碼實現(C語言)
#include
#include
#define MAXSIZE 10
typedef struct
{
int r[MAXSIZE];//存儲待排序數據
int length;//記錄順序表的長度
}Sqlist;
void swap(Sqlist *L,int i,int j)//交換數據函數
{
int temp = L->r[i];
L->r[i] = L->r[j];
L->r[j] = temp;
}
void print(Sqlist *L)//打印數據函數
{
int i;
for(i=0;i
printf("%d ",L->r[i]);
printf("\n");
}
void BubbleSort(Sqlist *L)//冒泡排序
{
int i,j;
for(i=0;i
{
for(j=L->length-1;j>=i;j--)
{
if(L->r[j]>L->r[j+1])
swap(L,j,j+1);
}
}
}
void BubbleSort2(Sqlist *L)//冒泡排序改進版1:增加標志位
{
int i,j;
int flag = 1;
for(i=0;i
{
flag = 0;
for(j=L->length-1;j>=i;j--)
{
if(L->r[j]>L->r[j+1])
{
swap(L,j,j+1);
flag = 1;
}
}
}
}
void BubbleSort3(Sqlist *L)//冒泡排序改進版2:雙向移動數據(雞尾酒排序)
{
int i,j;
for(i=0;i
{
for(j=i;j
{
if(L->r[j]>L->r[j+1])
swap(L,j,j+1);
}
for(j=L->length-1-(i+1);j>i;j--)
{
if(L->r[j]
swap(L,j-1,j);
}
}
}
void SelectSort(Sqlist *L)//直接選擇排序
{
int i,j,min;//min是當次循環的小值的下標
for(i=0;i
{
min=i;
for(j=i+1;j<=L->length;j++)
{
if(L->r[min]>L->r[j])
min=j;
}
if(i!=min)
swap(L,i,min);
}
}
void InsertSort(Sqlist *L)//直接插入排序
{
int i,j,tmp;
if(L->r[0]>L->r[1])//首先保證前2個元素有序,這樣后續元素才能插入
swap(L,0,1);
for(i=2;i<=L->length;i++)//插入L->r[i]元素
{
if(L->r[i]
{
tmp=L->r[i];
for(j=i-1;L->r[j]>tmp;j--)//將所有大于L->r[i]元素都后移,空出位置
L->r[j+1]=L->r[j];
L->r[j+1]=tmp;//插入正確位置
}
}
}
void QSort1(Sqlist *L,int left,int right)//快速排序
{
int i=left,j=right;
if(left>=right)
return;
int key = L->r[left];
while(i
{
while(L->r[j]>=key && i
j--;
L->r[i]=L->r[j];
while(L->r[i]<=key && i
i++;
L->r[j]=L->r[i];
}
L->r[i]=key;
QSort1(L,left,i-1);
QSort1(L,i+1,right);
}
/*快速排序算法第二種寫法*/
int Partition(Sqlist *L,int low,int high)
{
int pivotkey,tmp;
pivotkey=L->r[low];
tmp=pivotkey;
while(low
{
while(low
high--;
L->r[low]=L->r[high];
while(low
low++;
L->r[high]=L->r[low];
}
L->r[low]=tmp;
return low;
}
void QSort2(Sqlist *L,int low,int high)
{
int pivot;
if(low
{
pivot = Partition(L,low,high);
QSort2(L,low,pivot-1);
QSort2(L,pivot+1,high);
}
}
/*快速排序算法第二種寫法end*/
int main()
{
Sqlist data;
data.r[0]=9;data.r[1]=1;data.r[2]=5;data.r[3]=8;data.r[4]=3;data.r[5]=7;data.r[6]=4;data.r[7]=6;data.r[8]=2;data.r[9]=10;
data.length=sizeof(data.r)/sizeof(data.r[0]);
//BubbleSort(&data);
//BubbleSort2(&data);
//BubbleSort3(&data);
//SelectSort(&data);
//InsertSort(&data);
//QSort1(&data,0,data.length-1);
//QSort2(&data,0,data.length-1);
print(&data);
return 0;
}
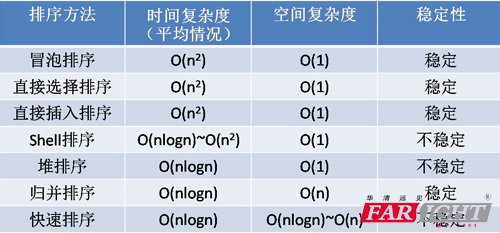
附錄2:各排序算法時間復雜度與空間復雜度對比