色yeye在线视频观看_亚洲人亚洲精品成人网站_一级毛片免费播放_91精品一区二区中文字幕_一区二区三区日本视频_成人性生交大免费看

整除性

一個整數能被另一個整數整除，記為 d|ad|a，意味著對某個整數 k，有a=kda=kd。

余數以及模運算

除法定理： 

對任意整數a和任意正整數n，存在唯一的整數q和r，滿足0<=r<n，并且a=qn+r。對任意整數a和任意正整數n，存在唯一的整數q和r，滿足0<=r<n，并且a=qn+r。 

取模運算：a % p（或a mod p），表示a除以p的余數。

比如給定一個正整數p，任意一個整數n，一定存在等式 ：n = kp + r ；其中 k、r 是整數，且 0 ≤ r < p，則稱 k 為 n 除以 p 的商，r 為 n 除以 p 的余數。

取模運算的規則如下：

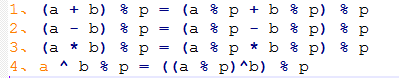
公約數性質

對任意整數 x 和 y，有： 

d|a并且d|b，則d|(ax+by)d|a并且d|b，則d|(ax+by) 

定義兩個不同時為 0 的整數 a 與 b 的最大公約數表示為 gcd(a,b)gcd(a,b)，如果 a 和 b 都不為 0，則 gcd(a,b)gcd(a,b) 為一個在 1 和 min(|a|,|b|)min(|a|,|b|) 之間的整數。定義 gcd(0,0)=0gcd(0,0)=0。其基本性質有如下幾條：

給出如下定理： 

如果a和b是不都為0的任意整數，則gcd(a,b)是a與b的線性組合{ax+by:x，y均屬于整數}中的最小元素。如果a和b是不都為0的任意整數，則gcd(a,b)是a與b的線性組合{ax+by:x，y均屬于整數}中的最小元素。 

歐幾里得算法

GCD遞歸定理

對于任意非負整數 a 和任意正整數 b，有 

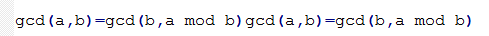
C語言實現歐幾里得算法:

歐幾里得算法的擴展形式

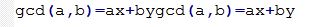
推廣歐幾里得算法以使其可以計算出相應的整系數 x，y。