��(d��ng)ǰλ�ã����(y��) > Ƕ��ʽ��Ӗ(x��n) > Ƕ��ʽ�W(xu��)��(x��) > �v������ > PID�㷨��C����?q��)��F(xi��n)��ʽ�����������T(m��n)
 PID�㷨��C����?q��)��F(xi��n)��ʽ�����������T(m��n)
�r(sh��)�g��2018-04-24 ��(l��i)Դ��δ֪
PID�㷨��C����?q��)��F(xi��n)��ʽ�����������T(m��n)
�r(sh��)�g��2018-04-24 ��(l��i)Դ��δ֪
һ��PID�㷨��(ji��n)��
��ˮ�ؿ���ģ�͡�����܇(ch��)��ِ�����S�w������(w��n)����ƽ��܇(ch��)�ٶȵȿ��ƌ�(sh��)�F(xi��n)�r(sh��)����?y��n)��A(y��)�O(sh��)ֵ�c��(sh��)�H����Ч��֮�g����һ����ƫ���(sh��)�Hݔ���c��(sh��)��(j��)����֮�g����һ�����ӕr(sh��)���������ܵõ�����Ŀ���Ч����PID���鑪(y��ng)�Þ�V����һ�N�Ԅ�(d��ng)���������ڌ�(sh��)�H�����м���PID�㷨�����_(d��)��ϵ�y(t��ng)�����`��׃����Ч����
������ᵽ�ĎN��(sh��)�������ԷQ(ch��ng)�����ϵ�y(t��ng)(�^(gu��)�̿��ƌ�(du��)�����“һ�����+������”�c“�������+������ ”���c(di��n),�f(shu��)���˾���푑�(y��ng)���t+�����ӕr(sh��))��PID��������һ�N�(y��u)��������
���˼�x��Pָ�DZ���(Proportion)��Iָ�Ƿe��(Integral)��Dָ��(Differential)����늙C(j��)�{(di��o)��ϵ�y(t��ng)�У�ݔ����̖(h��o)������Ҫ��늙C(j��)���D(zhu��n)�r(sh��)��������̖(h��o)Ҳ����(PID�㷨�r(sh��)���`��=ݔ��-����)��ͬ�r(sh��)늙C(j��)�D(zhu��n)��Խ�ߣ�������̖(h��o)Խ��Ҫ��㶮PID�㷨��ԭ�������ȱ��������P,I,D���Եĺ��x������Ҏ(gu��)�ɣ�
1.1����P
Proportion(����)������ݔ��ƫ�����һ��(g��)����(sh��)��
�����{(di��o)��(ji��)�����̞飺
y=Kp*e(t)
�{(di��o)��(ji��)����ݔ���cݔ��ƫ������ȡ������(xi��ng)�����䌍(sh��)���nj�(du��)�A(y��)�O(sh��)ֵ�ͷ���ֵ��ֵ�ķŴ�(sh��)��
�Dʾ
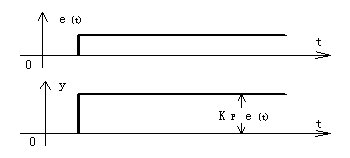
�D1 �����Ŵ�ʾ��D
���ƌ�(du��)���늙C(j��)�r(sh��)������KpԽ��r(sh��)��늙C(j��)�D(zhu��n)�ٻؚw��ݔ��ֵ���ٶȌ����죬���{(di��o)��(ji��)�`���Ⱦ�Խ�ߡ��Ķ�����Kpֵ�����Ԝp��?g��u)ķǷ�(w��n)�B(t��i)����(w��n)�B(t��i)�ĕr(sh��)�g������ͬ�r(sh��)Ҳ�������늙C(j��)�D(zhu��n)�����A(y��)�O(sh��)ֵ������ʎ�����Σ��������^(gu��)�ͣ��{(di��o)�����̫������Ƕ�C(j��)�D(zhu��n)��ϵ�y(t��ng)����(hu��)���F(xi��n)����܇(ch��)�u�[S��ǰ�M(j��n)���@����Kp�^(gu��)����ɵģ�����������e��I��Q�ˆ�(w��n)�}��
1.2 �e��I
Integral(�e��)���e��������ָ�{(di��o)��(ji��)����ݔ���cݔ��ƫ��ķe�ֳɱ��������á�
�e�ַ��̞飺

Ti�Ƿe�֕r(sh��)�g����(sh��)������ʾ�e���ٶȵĴ�С��TiԽ�e���ٶ�Խ�����e������Խ����
�Dʾ

�D2 �e���{(di��o)��(ji��)ʾ��D
�e�֭h(hu��n)��(ji��)���{(di��o)��(ji��)�����mȻ��(hu��)�����o�B(t��i)�`���Ҳ��(hu��)����ϵ�y(t��ng)��푑�(y��ng)�ٶȣ�Ҳ���Ƿe���(xi��ng)���{(di��o)��(ji��)�������@�Ĝ�����?y��n)�T(m��n)i�������Ǖr(sh��)�g����(sh��)��TiֵԽ�r(sh��)�gԽ�L(zh��ng)������Ч��Խ���@������ϵ�y(t��ng)�ij��{(di��o)�����e�ֳ���(sh��)T I Խ�e�ֵķe������Խ��������e�ֳ���(sh��)T I ��(hu��)�p���o�B(t��i)�`��������^(gu��)�̣������Ԝp�ٳ��{(di��o)�������ϵ�y(t��ng)�ķ�(w��n)���ԡ����ԣ���횸���(j��)��(sh��)�H���Ƶľ��wҪ���(l��i)�_��TI �����磺��(d��ng)��ֵ���Ǻܴ�r(sh��)�����ԜpС����Ч�����S��ԭϵ�y(t��ng)��ݔ��ֵ������߀��Ҫ��ƫ���M(j��n)�мӷ��e�ۡ���(d��ng)�@��(g��)���ۼӳ��^(gu��)�A(y��)��ֵ�r(sh��)����һ�����M(j��n)��̎�����Ķ��������l�����ƶ����F(xi��n)��ʎ�F(xi��n)��
1.3 ��D
Derivative(��)�����(xi��ng)�����䌍(sh��)������늙C(j��)�D(zhu��n)�ٵ�׃���ʡ�Ҳ����ǰ��ɴβ�ֵ�IJ
���{(di��o)��(ji��)�����ַ��̞�
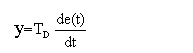
�Dʾ
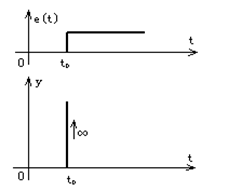
�D3 �ֿ���������
�ַ���(y��ng)��ƫ����̖(h��o)��׃��Ҏ(gu��)�ɣ������f(shu��)��׃��څ��(sh��)��ƫ�����(sh��)�Hƫ���׃�����ʣ�׃��Խ�죬���ֽ^��(du��)ֵԽ��ƫ������r(sh��)�����֞���;ƫ��pС�r(sh��)�����֞�ؓ(f��)��������ݔ�������ֲ����c�`����ֳ����ȣ���ӳ�˱�����׃����څ��(sh��)������(j��)ƫ����̖(h��o)��׃��څ��(sh��)��(l��i)�M(j��n)�г�ǰ�{(di��o)��(ji��)���Ķ�������ϵ�y(t��ng)�Ŀ����ԡ�TdֵԽ��ǰ�������þ͕�(hu��)Խ���@��������������ǰ���ơ������H�H��ƫ��ķŴ���������ʾ��(d��ng)ǰ�{(di��o)��(ji��)����(sh��)�������A(y��)�y(c��)ƫ���׃�����ஔ(d��ng)����ǰ�����˿��Ɣ�(sh��)��(j��)���ڱ������{(di��o)��(ji��)���У��܉���ǰ����ƫ�Ҳ�п��ܳ��F(xi��n)ؓ(f��)ֵ�������˶���ϵ�y(t��ng)�ij��{(di��o)�F(xi��n)��
һ��PID�㷨��(n��i)��
2.1 PID�㷨�x��
PID�㷨���б����e���{(di��o)��(ji��)(PI)���������{(di��o)��(ji��)��(PD)���ɸ���(j��)ϵ�y(t��ng)Ҫ���M(j��n)���x��ͨ�����˸����{(di��o)��(ji��)Ʒ�|(zh��)�������ѱ������e�֡������N���ýM������(l��i)���γ�PID�{(di��o)��(ji��)���������PID�ַ��̞飺
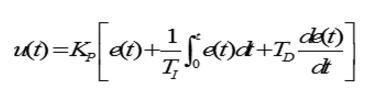
����u(t) �{(di��o)��(ji��)����ݔ����̖(h��o);
e(t) �{(di��o)��(ji��)����ƫ����̖(h��o)�������ڽo��ֵ�c�y(c��)��ֵ֮��
Kp ���������;
T i �e�֕r(sh��)�g
T d �֕r(sh��)�g
KP /T I �e��ϵ��(sh��)
KP / T D ��ϵ��(sh��)
2.2 PID�㷨Ҫ��
PID��Ҫ��һ��(g��)�]�h(hu��n)ϵ�y(t��ng)����(��ڰ�)���]�h(hu��n)ϵ�y(t��ng)���ڿ���ϵ�y(t��ng)�У��Ј�(zh��)��̎���Ԫ��ͬ�r(sh��)�����ݔ�뷴����Ԫ��늙C(j��)ϵ�y(t��ng)�У�����о��a�����y(c��)��늙C(j��)�Ȝy(c��)���O(sh��)�䡣����ϵ�y(t��ng)ԭ��D���£�
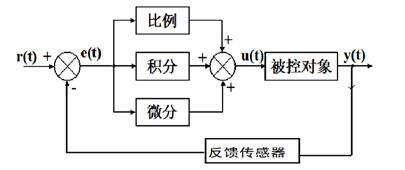
�D4 �]�h(hu��n)PID����ϵ�y(t��ng)
2.3 PID����(sh��)�������E��
��������(sh��)�����,��������;
���{(di��o)������e��,����������;
������ʎ���l��,�����̶�Ҫ�Ŵ�;
����Ư������(d��ng)��,�����̶�Ҫ��С;
����ƫ�x�؏�(f��)��,�e�֕r(sh��)�g��С��;
��������(d��ng)�����L(zh��ng),�e�֕r(sh��)�gҪ���L(zh��ng);
������ʎ��(d��ng)����,�֕r(sh��)�gҪ���L(zh��ng)��
һ��C���a��(sh��)�F(xi��n)
����Ӌ(j��)��C(j��)������һ�N�ɘӿ��ƣ���ֻ�ܸ���(j��)�ɘ��S�ɵ�ƫ��Ӌ(j��)�����������������ģ�M�����ǘ��B�m(x��)ݔ�����������M(j��n)���B�m(x��)���ơ���ô�����PID��ʽ����ֱ��ʹ�ã�����M(j��n)���xɢ��̎��
���O(sh��)�ɘӕr(sh��)�g�g����T(m��n)���t��k�r(sh��)�̣�
ƫ���e(k);
�e�֞�e(k)+e(k-1)+e(k-2)+...+e(0);
�֞�(e(k)-e(k-1))/T;
�Ķ���ʽ�xɢ�������£�
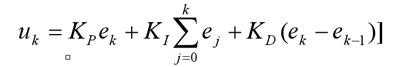
k �ɘ���̖(h��o)��k=0,1,2,…
u k ��k �βɘӕr(sh��)�̵�Ӌ(j��)��C(j��)ݔ��ֵ
e k ��k �βɘӕr(sh��)��ݔ���ƫ��ֵ
e k −1 ��k-1 �βɘӕr(sh��)��ݔ���ƫ��ֵ��
��(sh��)�H����Ĺ�ʽ��λ��ʽPID���\(y��n)���^�࣬ռ�Æ�Ƭ�C(j��)�YԴ��߀�����Ƴ�����ʽPID:
U(k) = P *e(k) + I *[e(k)+e(k-1)+...+e(0)]+ D *[e(k)-e(k-1)]��
��(ji��n)���������C�Z(y��)���Ќ�(xi��)�ɣ�
u(k) = u(k)-u(k-1) = Kp(e(k) - e(k-1)) + Ki *e(k) + Kd(e(k)) - 2e(k-1) + e(k-2))
����ı��_(d��)ʽ��������ʽ���_(d��)��ʽ��u(k)�c�������Ӌ(j��)��ƫ�����P(gu��n)��
C�Z(y��)��������a:
//��(chu��ng)��׃���Y(ji��)��(g��u)�w
struct pid_type{
float Kp; //PI�{(di��o)��(ji��)�ı�������(sh��)
float Ti; //PI�{(di��o)��(ji��)�ķe�ֳ���(sh��)
float T; //�ɘ�����
float Ki;
float ek; //ƫ��e[k]
float ek1; //ƫ��e[k-1]
float ek2; //ƫ��e[k-2]
float uk; //u[k]
signed int uk1; //��(du��)u[k]��������ȡ��
signed int adjust; //�{(di��o)��(ji��)��ݔ���{(di��o)����
}pid;
//׃����ʼ
void Pid_Init(void)
{
pid.Kp=4;
pid.Ti=0.005;
pid.T=0.001;
pid.Ki=0.6; //��ϵ��(sh��)Kd=KpTd/T������(j��)��(sh��)�H�{(di��o)��(ji��)
pid.ek=0;
pid.ek1=0;
pid.ek2=0;
pid.uk=0;
pid.uk1=0;
pid.adjust=0;
}
int PIDadjust(float ek) //PI�{(di��o)��(ji��)�㷨
{
if( gabs(ek)<0.1 )
{
pid.adjust=0;
}
else
{
pid.uk=pid.Kp*(pid.ek-pid.ek1)+pid.Ki*pid.ek; //Ӌ(j��)���������
pid.ek1=pid.ek;
pid.uk1=(signed int)pid.uk;
if(pid.uk>0)
{
if(piduk-piduk1>=0.5)
{
pi.uk1=pid.uk1+1;
}
}
if(piduk<0)
{
if(pid.uk1-pid.uk>=0.5)
{
pid.uk1=pid.uk1-1;
}
}
adjust=pid.uk1;
}
return adjust;
}
һ��С�Y(ji��)
�������ϵ��(sh��)Pһ�㌢�ӿ�ϵ�y(t��ng)��푑�(y��ng)�������o�����r�������ڜpС�o������^(gu��)��ı���ϵ��(sh��)��(hu��)ʹϵ�y(t��ng)�б��^��ij��{(di��o)�����a(ch��n)����ʎ��ʹ��(w��n)����׃�ġ�
����e�֕r(sh��)�gI�����ڜpС���{(di��o)���pС��ʎ��ʹϵ�y(t��ng)�ķ�(w��n)�������ӣ�����ϵ�y(t��ng)�o�������r(sh��)�g׃�L(zh��ng)��
�����֕r(sh��)�gD�����ڼӿ�ϵ�y(t��ng)��푑�(y��ng)�ٶȣ�ʹϵ�y(t��ng)���{(di��o)���pС����(w��n)�������ӣ���ϵ�y(t��ng)��(du��)�_��(d��ng)�����������p����
Ҳ�����f(shu��)����ϵ��(sh��)P�������F(xi��n)��,�����F(xi��n)���A(y��)�O(sh��)ֵ�c��(sh��)�H��ƫ��e�ִ������^(gu��)ȥ�����^(gu��)ȥTi�r(sh��)�g��(n��i)��ƫ��e�ۣ����Ԝp����ʎ����D������δ��(l��i)������(y��ng)��ƫ��׃���ʣ����Գ�ǰ�A(y��)�y(c��)��������ơ�
�@�����P(gu��n)PID�Y�ϵ��v�ķdz��ã����]�o��ң�
1. https://blog.csdn.net/u010312937/article/details/53363831#t3��PID�����㷨��C�Z(y��)�Ԍ�(sh��)�F(xi��n)<������>��
2. https://blog.csdn.net/qq229596421/article/details/51419813
3. https://blog.csdn.net/msdnwolaile/article/details/51038196
ף��ˬ!!
 11�¾͘I(y��)�L(f��ng)�ư�ح���н�Y18k����н11k�����¾͘I(y��)���c(di��n)
11�¾͘I(y��)�L(f��ng)�ư�ح���н�Y18k����н11k�����¾͘I(y��)���c(di��n) ʮ�¾͘I(y��)�L(f��ng)�ư�ح�x���A�� ��н�͘I(y��)�����ܶ����@
ʮ�¾͘I(y��)�L(f��ng)�ư�ح�x���A�� ��н�͘I(y��)�����ܶ����@ ���¾͘I(y��)�L(f��ng)�ư� | �͘I(y��)�΄�(sh��)���ԣ��A��W(xu��)�Ӆs���(sh��)����
���¾͘I(y��)�L(f��ng)�ư� | �͘I(y��)�΄�(sh��)���ԣ��A��W(xu��)�Ӆs���(sh��)���� ����T�ܿɐ�(��i) ���YҲ���� 8��н�Y���t
����T�ܿɐ�(��i) ���YҲ���� 8��н�Y���t ��һ�N���������e�˼ҵij���T����һ�N���YҲ�����e��
��һ�N���������e�˼ҵij���T����һ�N���YҲ�����e�� ���¾͘I(y��)�L(f��ng)�ư�|��һ�Q���@��(g��)��Ƹ��(bi��o)��(zh��n)���Ҷ��M(j��n)����(l��i)��
���¾͘I(y��)�L(f��ng)�ư�|��һ�Q���@��(g��)��Ƹ��(bi��o)��(zh��n)���Ҷ��M(j��n)����(l��i)�� ��н20W��С����(l��i)�� �����@Щ��(j��ng)�(y��n)�����f(shu��)�o�� (t��ng)
��н20W��С����(l��i)�� �����@Щ��(j��ng)�(y��n)�����f(shu��)�o�� (t��ng) ���Ͼ��������13K�q��16K ��Ȼ����Ů�ώ����P(gu��n)
���Ͼ��������13K�q��16K ��Ȼ����Ů�ώ����P(gu��n) (t��ng)��ǰ����һ����н15W��С����(l��i)�v����н�v���ˣ�
(t��ng)��ǰ����һ����н15W��С����(l��i)�v����н�v���ˣ� ���H�����ң��ٲ���ؓ(f��)�ഺ�ˣ�
���H�����ң��ٲ���ؓ(f��)�ഺ�ˣ� 19�î��I(y��)����ǰ�ҵ�������߀����н15W���ǷN����ţ�ˣ�
19�î��I(y��)����ǰ�ҵ�������߀����н15W���ǷN����ţ�ˣ� ܊���D(zhu��n)�Ё�(l��i)�W(xu��)Ƕ��ʽ���c�A��Y(ji��)�²���֮��
܊���D(zhu��n)�Ё�(l��i)�W(xu��)Ƕ��ʽ���c�A��Y(ji��)�²���֮�� �A���h(yu��n)Ҋ(ji��n)90+�(xi��ng)Ŀ�@����������2021���
f(xi��)ͬ�����(xi��ng)Ŀ��
�A���h(yu��n)Ҋ(ji��n)90+�(xi��ng)Ŀ�@����������2021���
f(xi��)ͬ�����(xi��ng)Ŀ�� �A���h(yu��n)Ҋ(ji��n)�s�@2021�vӍ��������ȿڱ�Ӱ����I(y��)����Ʒ
�A���h(yu��n)Ҋ(ji��n)�s�@2021�vӍ��������ȿڱ�Ӱ����I(y��)����Ʒ �A���h(yu��n)Ҋ(ji��n)��������2021����h���k��У��Ϣ�W(xu��)�ƺ���(li��n)��
�A���h(yu��n)Ҋ(ji��n)��������2021����h���k��У��Ϣ�W(xu��)�ƺ���(li��n)�� ��ůͬ�й���(chu��ng)�ѿ�(j��) 2019�A���h(yu��n)Ҋ(ji��n)�����������(hu��)���ع�
��ůͬ�й���(chu��ng)�ѿ�(j��) 2019�A���h(yu��n)Ҋ(ji��n)�����������(hu��)���ع� ������УAI�˹����܌W(xu��)�ƽ��O(sh��) �A���h(yu��n)Ҋ(ji��n)�˹������Y��
������УAI�˹����܌W(xu��)�ƽ��O(sh��) �A���h(yu��n)Ҋ(ji��n)�˹������Y�� �A���h(yu��n)Ҋ(ji��n)���������Ĵ�ʡ��(li��n)�W(w��ng)���(hu��)���s�@��(y��u)����I(y��)��(zhu��n)��
�A���h(yu��n)Ҋ(ji��n)���������Ĵ�ʡ��(li��n)�W(w��ng)���(hu��)���s�@��(y��u)����I(y��)��(zhu��n)��